what is meant by unbalanced assignment problem

the intact one

Read MBA, BBA, B.COM Notes

Unbalanced Assignment Problems

Whenever the cost matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix. The dummy rows or columns will contain all costs elements as zeroes. The Hungarian method may be used to solve the problem.

Example :  A company has five machines that are used for four jobs. Each job can be assigned to one and only one machine. The cost of each job on each machine is given in the following Table.

Unbalanced Maximization Assignment problem example

Assignment Problem

Solution:  Convert the 4 × 5 matrix into a square matrix by adding a dummy row D5.

Dummy Row D5 Added

Row-wise Reduction of the Matrix

Column-wise reduction is not necessary since all columns contain a single zero. Now, draw minimum number of lines to cover all the zeros, as shown in Table.

All Zeros in the Matrix Covered

Number of lines drawn ≠ Order of matrix. Hence not optimal.

Select the least uncovered element, i.e., 1, subtract it from other uncovered elements, add to the elements at intersection of lines and leave the elements that are covered with single line unchanged as shown in Table.

Subtracted or Added to Elements

Again Added or Subtracted 1 from Elements

Number of lines drawn = Order of matrix. Hence optimality is reached. Now assign the jobs to machines, as shown in Table.

Assigning Jobs to Machines

Example :  In a plant layout, four different machines M1, M2, M3 and M4 are to be erected in a machine shop. There are five vacant areas A, B, C, D and E. Because of limited space, Machine M2 cannot be erected at area C and Machine M4 cannot be erected at area A. The cost of erection of machines is given in the Table.

Find the optimal assignment plan.

Solution:  As the given matrix is not balanced, add a dummy row D5 with zero cost values. Assign a high cost H for (M2, C) and (M4, A). While selecting the lowest cost element neglect the high cost assigned H, as shown in Table below.

– Row-wise reduction of the matrix is shown in Table.

Matrix Reduced Row-wise

Note:  Column-wise reduction is not necessary, as each column has at least one single zero. Now, draw minimum number of lines to cover all the zeros, see Table.

Lines Drawn to Cover all Zeros

Number of lines drawn ≠ Order of matrix. Hence not Optimal. Select the smallest uncovered element, in this case 1. Subtract 1 from all other uncovered element and add 1 with the elements at the intersection. The element covered by single line remains unchanged. These changes are shown in Table. Now try to draw minimum number of lines to cover all the zeros.

Added or Subtracted 1 from Elements

Now number of lines drawn = Order of matrix, hence optimality is reached. Optimal assignment of machines to areas are shown in Table.

Optimal Assignment

Hence, the optimal solution is:

Share this:

You might also like, security professionals and organisations, identifying training and development need, designing training programs, information management for global logistics, 2 thoughts on “ unbalanced assignment problems ”.

• Pingback: GGSIPU(NEW DELHI) QUANTITATIVE TECHNIQUE – 2ND SEMESTER – STUDY MBA & BBA NOTES
• Pingback: CCSU(BBA) 406 Operation Research – Home | Management

Leave a Reply Cancel reply

You must be logged in to post a comment.

FYBMS, SYBMS, TYBMS and beyond BMS

What is Balanced or Unbalanced Assignment problem?

Operations Research

The Assignment problem can be Balanced or Unbalanced problem.

A Balanced problem means the no. of rows and no. of columns in the problem are equal. E. g. if the problem contains 4 workers and 4 jobs, then it is balanced.

Where as, an Unbalanced problem means the no. of rows and no. of columns are not equal. E. g. if the problem contains 4 workers and 3 jobs it is not balanced. Then first we need to balance the problem by taking a Dummy job (imaginary job).

Like it? Share with your friends!

Posted by Score Tutorial

Cancel reply.

You must be logged in to post a comment.

Facebook comments:

forgot password

New Revamp Offer - Upto 30% OFF !!!

New upto 30% off .

Please Login

• HR Management Assignment Help
• Supply Chain Management Assignment Help
• Conflict Management Assignment Help
• Marketing Management Assignment Help
• Write My Project Management Assignment
• Write My Management Assignment
• Strategy Assignment Help
• Porter’s Five Forces Marketing Assignment Help
• Personal Finance Assignment Help
• Corporate Finance Planning Assignment Help
• Nursing Assignment Help
• Psychology Assignment Help
• History Assignment Help
• Sociology Assignment Help
• Social Science Assignment help
• Philosophy Assignment Help
• Public Relations Assignment Help
• Contract Law Assignment Help
• Commercial Law Assignment Help
• Business Law Assignment Help
• Corporate Law Assignment Help
• Taxation Law Assignment Help
• Constitutional Law Assignment Help
• Company Law Assignment Help
• Accounting Assignment Help
• Managerial Economics Assignment Help
• Microeconomics Assignment Help
• Macroeconomics Assignment Help
• Cheap Assignment Writing Service
• Electronics Engineering Assignment Help
• Mechanical Engineering Assignment Help
• Civil Engineering Assignment Help
• MYOB Assignment Help
• Do My Assignment Online
• Urgent Assignment Help
• Dissertation Help
• Essay Assignment Help
• Cheap Essay Writing Service
• Cost Accounting Homework Help
• Managerial Accounting Homework Help
• Maths Homework Help
• Java Programming Assignment Help
• PHP Programming Assignment Help
• Javascript Programming Assignment Help
• Online C++ Programming Assignment Help
• C# Programming Assignment Help
• Android Programming Assignment Help
• MATLAB Assignment Help
• Research Paper Help
• Thesis Help
• Buy Case Study Assignment
• Hire Case Study Writers
• Write My Case Study
• CDR Writing Help
• Custom Coursework Assignment Help
• My Assignment Help
• My Assignment Services
• All Assignment Help
• Instant Assignment Help
• Assignment Help Melbourne
• Assignment Help Perth
• Assignment Help Sydney
• Assignment Writing Help Dubai
• Dissertation Help UAE

New Zealand

• FREE SAMPLES

• Assignment Help

What Is An Unbalanced Assignment Problem? How It Is Solved With Hungarian Method

An assignment problem is a combination of optimization problems which occurs in the field of operations research. It is a special case and is the degenerate form of a transportation problem when each supply is 1 and each demand is 1. When a particular work is assigned to an agent or it involves assigning a number of tasks to an equal number of agents and these agents can be people, machines, vehicles and plants, etc. and the objective is to increase the total profit or minimize the total cost. The process can be applicable in different fields like assigning personnel to offices, machines to jobs, teachers to classes or salesmen to sales territories. Before we study more on this topic, we want to inform you that we have assignment services where you get assignments on more than 180+ subjects through top-notch experts at GotoAssignmentHelp platform. We provide assignments, essays, thesis help , and many more so join now on GotoAssignmentHelp platform to avail our services.

The assignment problem being a special case of transportation problem can be solved by transportation technique or simplex method (North-West corner rule, least cost method, Vogel’s approximation method, etc.). The most common and popular method to solve assignment problems is the Hungarian method which was developed and published by H.W. Kuhn. The Hungarian method was so named because the algorithm was based on the works of two Hungarian mathematicians: D. Konig and J. Egervary. Later the algorithm was reviewed and observed by James Munkres and was found to be strongly polynomial. The simplex method for linear programming was also followed to solve the assignment problem. The unbalanced assignment problem was solved by Kore’s new method that was proposed by him which was based on generating “ones” instead of “zeros” in the matrix. Many algorithms for solving cost minimization and profit maximizing assignment problems was investigated by Abdur Rashid. Sometimes, in assignment problems, the number of agents is not equal to the number of tasks and these problems are known as unbalanced assignment problems. Then the matrix will not be a square matrix and with these types of sums, the traditional method was to consider costs in such rows or columns as zero. After forming a balanced equation, the problem could be solved by the Hungarian method. If you find assignments and their numerical difficulties, the experts of GotoAssignmentHelp can help you solve them with the best tricks.

As the assignment problem is a special case of transportation problem it can be formulated as a linear programming problem where you have to take n tasks and solve them with n agents. Each agent has to complete only one task through this solving method. Here one should take the first set of constraints as an agent and the second set of constraints as a task. From many formulations, it is pointed out that the assignment problem is a 0-1 integer programming problem. You have to make a matrix of n x n type with a i = b j = 1. If you have problems with assignments, homework , thesis, case studies, avail our expert help from GotoAssignmentHelp.

Hungarian method

In hungarian method you have to solve by the following steps:.

Step 1: You have to determine the total opportunity cost matrix: the minimum element from each row of the given matrix should be subtracted from the elements of the respective rows and then continue the same with the column. The minimum element from each column of the matrix should be subtracted from the elements of the respective columns. Through this process, you obtain a total opportunity cost matrix.

Step 2: The minimum number of horizontal and vertical lines should be drawn to cover all the zeros obtained in the total opportunity cost matrix. If the order of the matrix is maintained then an optimal assignment can be made by the usual procedure so that the total opportunity cost involved is zero. And if the number of lines drawn is less than the order of the payoff matrix follows the next step.

Step 3: The uncovered element in the current total opportunity cost matrix should be the smallest. Then this smallest element should be subtracted from all the uncovered elements and be added at the intersection of the vertical and horizontal lines. Thus, you obtain a total opportunity cost matrix.

Step 4: repeat process 2 and 3 until you get total opportunity cost zero.

There are various numerical illustrations which you will find on our site, GotoAssignmentHelp for understanding the theory better so if you are having problems in assignment help , essays and homework you can reach us. We have a group of experts who are highly qualified and take urgent assignments so that you can relax. We also offer these assignments at affordable prices.

RELATED ARTICLES MORE FROM AUTHOR

7 Useful Tips For Referencing Your Academic Assignment

7 Advantages of Assignments That Every Student Should Know

Top 12 Factors and Approaches Which Affect Your Assignment

• Assignment Help 118
• writing tips 41
• Essay Help 32
• Exam Tips 20
• success tips 16
• Research Paper Help 16

Featured Posts

• All time popular

(256) 666-6597

Get 20% OFF + 5% cashback on your first order

Get 25% OFF + 5% cashback on your first order

One stop destination for students from Australia, UK, USA and all over the world for the best online assignment help services.

GotoAssignmentHelp, the online assignment writing company provides the best online assignment help service for students from K9- PhD.

Useful Links

Question Bank

What is the enemy of #creativity?

100% Secure Payment

All the information and papers on this website GotoAssignmentHelp.com is published in good faith and for research and reference purposes only. We do not allow submitting these papers as it is for academic credit.

Copyright © GotoAssignmentHelp.com 2019

• Privacy Policy
• Refund Policy
• Terms of Use

Unbalanced Assignment Problem

In the previous section, the number of persons and the number of jobs were assumed to be the same. In this section, we remove this assumption and consider a situation where the number of persons is not equal to the number of jobs . In all such cases, fictitious rows and/or columns are added in the matrix to make it a square matrix.

• Maximization Problem
• Multiple Optimal Solutions

Example: Unbalanced Assignment Problem

Since the number of persons is less than the number of jobs, we introduce a dummy person (D) with zero values. The revised assignment problem is given below:

Use Horizontal Scrollbar to View Full Table Calculation.

Now use the Hungarian method to obtain the optimal solution yourself. Ans. = 20 + 17 + 17 + 0 = 54.

Share and Recommend

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

Linear assignment with non-perfect matching

Dec 8, 2020

The linear assignment problem (or simply assignment problem) is the problem of finding a matching between two sets that minimizes the sum of pair-wise assignment costs. This can be expressed as finding a matching (or independent edge set) in a bipartite graph \(G = (U, V, E)\) that minimizes the sum of edge weights. The edge weights may be positive or negative and the bipartite graph does not need to be complete : if there is no edge between two vertices then they cannot be associated. Note that a maximum-weight assignment can be obtained by negating the weights and finding a minimum-weight assignment.

The simplest form of the assignment problem assumes that the bipartite graph is balanced (the two sets of vertices are the same size) and that there exists a perfect matching (in which every vertex has a match). Let \(n\) be the number of elements in each set and let \(C\) be a square matrix of size \(n \times n\) that contains the edge weights. Missing edges are represented by \(\infty\), such that \(C_{i j} < \infty \Leftrightarrow (i, j) \in E\). The assignment problem can then be clearly expressed as an integer linear program : (note that the problem is not actually solved using a general-purpose ILP solver, it is just a convenient framework in which to express the problem)

The constraint that the sum of each row and column is equal to one ensures that each element has exactly one match. However, what happens when the graph is not balanced or does not contain a perfect matching? We cannot enforce the sums to be equal to one. Which problem should be solved?

I recommend reading the tech report “On Minimum-Cost Assignments in Unbalanced Bipartite Graphs” by Lyle Ramshaw and Robert E. Tarjan. I will summarize some of the main points here.

Let us consider a more general, rectangular problem of size \(r \times n\) and assume (without loss of generality) that \(r \le n\). If \(r = n\) then the problem is balanced, if \(r < n\) it is unbalanced.

Clearly an unbalanced probem cannot have a perfect matching, since there will be at least \(n - r\) unmatched elements in the larger set. However, it may be possible to find a matching in which every vertex in the smaller set has a match. This is referred to as a one-sided perfect matching and the optimization problem can be expressed:

The inequality constraints enforce that each element in the smaller set has exactly one match while each element in the larger set has at most one match. Ramshaw and Tarjan outline a method to reduce from an unbalanced problem to a balanced problem while preserving sparsity. A simple alternative is to add \(n - r\) rows of zeros and then exclude these edges from the eventual solution. Most libraries for the assignment problem solve either the balanced or unbalanced version of this problem (see the later section).

However, whether balanced or unbalanced, it may still occur that the constraint set is infeasible, meaning that there does not exist a (one-sided) perfect matching. Let \(\nu(W) \le r\) denote the size of the largest matching in the graph. If \(\nu(W) < r\), then there does not exist a one-sided perfect matching and all possible matchings are imperfect.

Ramshaw and Tarjan actually outline three different versions of the assignment problem:

• perfect matching
• imperfect matching
• minimum-weight matching

The imperfect matching problem is to find the matching of size \(\nu(G)\) with the minimum cost. The minimum-weight matching problem is to find the matching of any size with the minimum cost. If \(\nu(G) = r = n\), then perfect and imperfect matching coincide. Otherwise, when \(\nu(G) < n\), there does not exist a perfect matching.

The imperfect matching problem can be expressed

and the minimum-weight matching problem can be expressed

Ramshaw and Tarjan show that both of these problems can be reduced to finding a perfect matching in a balanced graph. When using linear assignment, we should carefully consider which of the three problems we actually want to solve.

In support of minimum-weight matching

The minimum-weight matching problem is often the most natural choice, since it puts no constraint on the size of the matching. To illustrate the difference between this and the other problems, consider the following balanced problem:

The solution to perfect (or imperfect) matching is to choose -1 and -2 for a total score of -3 and a cardinality of 2. The solution to minimum-weight matching is to choose -4 with a cardinality of 1.

Minimum-weight matching will never select an edge with positive cost: it is better to simply leave it unselected. Edges with zero cost have no impact.

It may be more natural to consider the maximization of positive weights than the minimization of negative costs.

Min-cost imperfect matching with positive weights

Be careful when solving imperfect matching problems with positive edge weights! I would avoid this situation altogether due to the tension that exists between maximizing the number of matches and minimizing the sum of (positive) costs. This may result in the unexpected behaviour that adding an edge to the graph increases the minimum cost. For example, compare the following two problems:

Quick and dirty transformations

Ramshaw and Tarjan above describes some clever techniques to transform imperfect and minimum-weight matching problems into perfect matching problems while preserving sparsity. Here we describe some quick and dirty alternatives.

We can always transform an unbalanced (and therefore imperfect) problem into a balanced problem by adding \(n - r\) rows of zeros. The resulting balanced graph has a perfect matching if and only if the original unbalanced graph had a matching of size \(r\) (in which every vertex in the smaller set is matched).

If we need to solve imperfect matching but we only have a solver for perfect matching, it suffices to replace the infinite edge weights with a large, finite cost (e.g. larger than the total absolute value of all weights). The resulting graph must contain a perfect matching since it is a complete bipartite graph, and each high-cost edge is worth more than all original edges combined. The high-cost edges can be excluded at the end.

Most existing packages either solve perfect, one-sided perfect or imperfect matching. To use one of these solvers for the minimum-weight matching problem, it suffices to replace all positive edges (including infinite edges) with zero. If using a solver that leverages sparsity, it is better to use the technique described by Ramshaw and Tarjan.

Python packages

The table below outlines the different behaviour of several popular packages. The code that was used to determine the behaviour is available as a Jupyter notebook .

Assignment Problem: Meaning, Methods and Variations | Operations Research

After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:

An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.

The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.

Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.

Definition of Assignment Problem:

ADVERTISEMENTS:

Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.

The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:

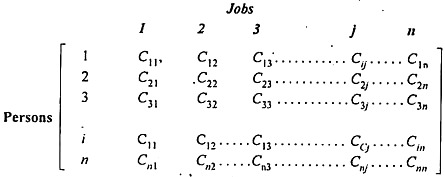
Variations of the Assignment Problems:

Unbalanced Assignment Problem:

Any assignment problem is said to be unbalanced if the cost matrix is not a square matrix, i.e. the no of rows and the no of columns are not equal. To make it balanced we add a dummy row or dummy column with all the entries is zero.

There are four jobs to be assigned to the machines. Only one job could be assigned to one machine are given in following matrix.

Recommended for you

Students also viewed.

• Note about Decision making
• Note about Inventory control
• Critical path method and PERT
• Sequencing problem and replacement theory
• Note about Game theory
• Note about Assignment problem-balanced

Related documents

• Transportation problems - optimality test
• Note about Transportation problems
• Linear programming -Duality
• Linear programming problems - simplex method
• Linear programming problems
• Introduction to operations research

Preview text

Operations Research

Notes Unit 8: Assignment Problem – Unbalanced

Introduction.

8 Variations of the Assignment Problem

8 Multiple Optimal Solutions

8 maximization assignment problems, 8 unbalanced assignment problem.

8 Routing Problems/Travelling Salesman Problems 8.5 Steps to Resolve Looping in Travelling Salesman Problem

8 Review Questions

8 Further Readings

After studying this unit, you will be able to:

 Know about variations of the assignment problem

 Learn how to solve an unbalanced assignment problem, profit maximization problem etc.

 Understand how to solve a travelling salesman problem

The basic objective of an assignment problem is to assign n number of resources to n number of activities so as to minimize the total cost or to maximize the total profit of allocation in such a way that the measure of effectiveness is optimized.

The problem of assignment arises because available resources such as men, machines, etc., have varying degree of efficiency for performing different activities such as job. Therefore cost, profit or time for performing the different activities is different. Hence the problem is, how should the assignments be made so as to optimize (maximize or minimize) the given objective.

The assignment model can be applied in many decision-making processes like determining optimum processing time in machine operators and jobs, effectiveness of teachers and subjects, designing of good plant layout, etc. This technique is found suitable for routing traveling salesmen to minimize the total traveling cost, or to maximize the sales.

In this unit you will learn how to solve special types of assignment problems such as unbalanced problems, travelling salesman problem etc.

Unit 8: Assignment Problem – Unbalanced

8 Variations of the Assignment Problem Notes

There can be many types of variations in a assignment problem. In this unit we will discuss in detail about the various types of assignment problem you may encounter in the real life scenario.

In this unit, we will discuss on following four variations of the assignment problem:

Multiple Optimal Solutions

Maximization case in assignment problems

Unbalanced Assignment problem

Travelling Salesman Problem

While making an assignment in the reduced assignment matrix, it is possible to have two or more ways to strike off a certain number or zeroes. Such a situation indicates multiple optimal solutions with the same optimal value of objective function. In such cases the more suitable solution may be considered by the decision maker.

Notes If the assignment problem has only one solution then the solution is said to be

Unique solution ****.

In maximization problem, the objective is to maximize profit, revenue, etc. Such problems can be solved by converting the given maximization problem into a minimization problem.

Change the signs of all values given in the table or another method is,

Select the highest element in the entire assignment table and subtract all the elements of the table from the highest element.

Alpha Corporation has 4 plants, each of which can manufacture any one of the 4 products. Production cost differs from one plant to another plant, so also the sales revenue. Given the revenue and the cost data below, obtain which product each plant should produce to maximize the profit.

Sales revenue ( ` in 000s) Product 1 2 3 4 A 50 68 49 62 B 60 70 51 74 C 55 67 53 70

D 58 65 54 69

Step 6: Determination of profit associated with the assignment. Notes

Plant Product Total Profit (Rs.) 2 4 1 3

Total Profit 22,

When negative signs are used to make the optimal assignment.

Step 1: Profit matrix with (–)ve signs.

Product 1 2 3 4 A –1 –8 –4 – B –5 –7 –6 – C –3 –5 –4 –

D –3 –1 –6 –

Step 2: Row-wise reduction of the matrix.

Product 1 2 3 4 A 7 0 4 7 B 2 0 1 2 C 2 0 1 3

Step 3: Column-wise reduction of the matrix.

Product 1 2 3 4 A 5 0 4 5 B 0 0 1 0 C 0 0 1 1

Step 4: Trial assignment.

Step 5: determine of profit associated with the assignment..

Plant Product Total Profit ( ` ) 2 4 1 3

Notes Inference

Hence to get a maximum profit of ` 22,000, Alpha Corporation should produce 2 products in plant A, B should manufacture product 4, C plant should manufacture product 1 and D plant should manufacture product 3.

Example: A company has 4 territories and 4 salesmen available for assignment. The territories are not equally rich in their sales potential; it is estimated that a typical salesman operating in each territory would bring in the following annual sales:

Territory I II III IV Annual Sales (`) 60,000 50,000 40,000 30, Four salesmen are also considered to differ in their ability. It is estimated that working under the same conditions, their yearly sales would be proportionately as follows:

Salesmen A B C D Proportion 7 5 5 4 If the criterion is the maximum expected total sales cum the intuitive answer is to assign the best salesman to the richest territory, the next best salesman to the second richest and so on. Verify this answer by assignment model.

Step 1: Matrix showing the proportion of sales revenue.

Territory (in’000) I (6) II (5) III (4) IV (3) A (7) 42 35 28 21 B (5) 30 25 20 15 C (5) 30 25 20 15

D (4) 24 20 16 12

Step 2: calculation of sales revenue associated with the assignment based on intuition..

Salesman Territory Total Profit ( ` ) I II/III III/II IV

Step 3: Verification of the results intuitively found with the use of assignment model.

Conversion of sales revenue matrix into cost matrix.

Territory I II III IV A 0 7 14 21 B 12 17 22 27 C 12 17 22 27

D 18 22 26 30

Notes Step 4: Trial assignment.

Territory I II III IV A 0 2 4 6 B 0 0 0 1 C 0 0 0 1

Step 5: Calculation of total sales revenue.

Salesman Territory Total Sales Revenue (Rs. ) A B C D

Thus, by following the above assignment schedule for allocating the territories to the 4 salesmen, the sales revenue can be maximized to ` 99,000.

Task A marketing manager has 5 salesman and 5 sales districts. Considering the capabilities of the salesman and the nature of the districts, the marketing manager estimates that sales per month (in, 00 `) for each salesman in each district would be as follows:

A B C D E 1 32 38 40 28 40 2 40 24 28 21 36 3 41 27 33 30 37 4 22 38 41 36 36 5 29 33 40 35 39

Find the assignment that will result in maximum sale.

Self Assessment

Multiple Choice Questions:

• An assignment problem will have the following solution:

(a) optimal (b) unique

(c) multiple (d) all of the above

• Maximisation assignment problem is transformed into minimization problem by

(a) adding each entry in a column from the maximum value in that column

(b) subtracting each entry in a column from maximum value in that column

(c) subtracting each entry in the table from the maximum value in that table

(d) any one of the above

• When an assignment problem has more than one solution, then it is Notes

(a) Multiple Optimal solution (b) The problem is unbalanced

(c) Maximization problem (d) Balanced problem

If the given matrix is not a square matrix, the assignment problem is called an unbalanced problem. In such type of problems, add dummy row(s) or column(s) with the cost elements as zero to convert the matrix as a square matrix. Then the assignment problem is solved by the Hungarian method.

Example: A company has 4 machines to do 3 jobs. Each job can be assigned to 1 and only 1 machine. The cost of each job on a machine is given to the following table:

Machines W X Y Z A 18 24 28 32 B 8 13 17 18

C 10 15 19 22

What are the job assignments which will minimize the cost?

Step 1: Conversion of the above unbalanced matrix into a balanced matrix.

Machines W X Y Z A 18 24 28 32 B 8 13 17 18 C 10 15 19 22

Using reduction rules

Machines W X Y Z A 0 6 10 14 B 0 5 9 10 C 0 5 9 12

Note: It is apparent from the above matrix that it is not possible to reduce the matrix column-wise. Hence, Hungarian approach is used.

Solution: Notes

Step 1: Conversion of the unbalanced matrix into a balanced matrix.

Job A B C D E 1 6 7 5 10 8. 2 7 8 6 7 5. 3 8 9 11 7 8. 4 4 6 8 7 8.

5 0 0 0 0 0

Step 2: Conversion of maximisation matrix into a minimization case.

Job A B C D E 1 –6 –7 –5 –10 –8. 2 –7 –8 –6 –7 –5. 3 –8 –9 –11 –7 –8. 4 –4 –6 –8 –7 –8.

Step 3: Conversion of above matrix into an effective matrix.

Job A B C D E 1 3 2 5 0 1. 2 1 0 2 1 2. 3 2 1 0 4 3. 4 3 2 0 1 0.

It is apparent that in the above matrix the reduction rules cannot be applied hence direct Hungarian

approach is followed. Step 4: Hungarian approach is applied.

L 1 L 2 L 3 L 4

Notes Step 5: Trial assignment.

Job A B C D E 1 3 2 5 0 1. 2 0 0 2 1 1. 3 1 1 0 4 2. 4 3 2 0 1 0

5 0 0 0 0 0.

Step 6: Calculation of maximum profit for the assignment.

From To Total Sales ( ` ) A B C D E

Total profit 37.

The maximum total profit for the assignment is ` 37. And the job to be declined is A as the machinist available 5th is supposed to be fictitious.

Fill in the blanks:

If the given matrix is not a ............, the assignment problem is called an unbalanced problem

A dummy row(s) or column(s) with the cost elements as .............. is added to convert the matrix of an unbalanced assignment problem as a square matrix.

A given assignment problem can be classified into balanced or unbalanced on the basis of ........................

8 Routing Problems/Travelling Salesman Problems

A salesman, who wishes to travel through his territory visiting various cities, wishes to visit one city only once and wants to come back to the city from where be started and then go to other cities one after other. As he is a single person who has to visit various cities, mere Reduction Theorem Rules or Hungarian approach would not help in arriving at optimum solution always. Hence, a modified solution would be found out to arrive at an optimal solution.

Notes 4. Modified Matrix – 2.

To From 1 2 3 4 5 I - 0 1 0 0 II 0 - 0 0 1 III 2 2 - 6 0 IV 0 0 2 - 3 V 2 0 0 6 -

The routes chosen for journey are: Alternative - I Alternative - II From To From To I 2 I 4 II 4 II 1 III 5 III 5 IV 1 IV 2 V 3 V 3

Note: In both the solutions, there is looping, Hence, it is not an optimum solution to travelling salesman problem. Hence, it is to be improved further.

8.5 Steps to Resolve Looping in Travelling Salesman Problem

Choose the next minimum uncovered element in the reduced matrix. If there are more than one such numbers, all the possible alternatives are to be tried until an unique optimum solution is found out.

Check whether looping is present in modified matrix after trial assignment. Modified matrix having no looping is an optimum solution.

Did u know? The TSP has several applications even in its purest formulation, such as planning, logistics, and the manufacture of microchips. Slightly modified, it appears as a sub-problem in many areas, such as DNA sequencing. In these applications, the concept city represents, for example, customers, soldering points, or DNA fragments, and the concept distance represents travelling times or cost, or a similarity measure between DNA fragments. In many applications, additional constraints such as limited resources or time windows make the problem considerably harder.

Example: A travelling sales man has to visit 5 cities. He wishes to start form a particular city visit each city once and then return to his starting point. The travelling time (in hours) for each city from a particular city is given below:

To Notes A B C D E From a  4 7 3 4 b 4  6 3 4 c 7 6  7 5 d 3 3 7  7 e 4 4 5 7 

What should be the sequence of visit of the salesman, so that the total travelled time is minimum.

Application of Reduction Theorem Rules

(1) Row-wise Reduced Matrix

a  1 4 0 1 b 1  2 0 1 c 2 1  2 0 d 0 0 4  4 e 0 0 1 3 

(2) Column-wise Reduced Matrix

a  1 3 0 1 b 1  1 0 1 c 2 1  2 0 d 0 0 3  4 e 0 0 0 3 

(i) Modified Matrix – 1

a - 0 1 0 0 b 0 - 0 0 1 c 2 2 - 6 0 d 0 0 2 - 3 e 2 0 0 6 -

(6) Modified Matrix 2. Notes

a  0 2 0 1 b 0  0 0 1 c 1 0  2 0 d 0 0 3  5 e 0 0 0 4 

(7) Calculation of Minimum Total Time Required for Travelling.

From To Travelling Time (Hours) a E 4 b D 3 c B 6 d A 3 e C 5 Total Time 21

The minimum time required to complete the travel programme with the above unique solution works out to be 21 hours.

Example: A salesman has to visit 4 cities A, B, C, and D. The distance (100 kms) between

4 cities is:

To From A B C D a - 4 7 3 b 4 - 6 3 c 7 6 - 7 d 3 3 7 -

If the salesman starts from city 'A' and comes back to city 'A', which route should he select so that total distance travelled by him is minimum?

(1) Row-wise Reduced Matrix.

a - 1 4 0 b 1 - 3 0 c 1 0 - 1 d 0 0 7 -

Notes (2) Column-wise Reduced Matrix.

a - 1 1 0 b 1 - 0 0 c 1 0 - 1 d 0 0 4 -

(3) The Route Chosen for Journey are:

From To Journey Time a D 3 b C 6 c B 6 d A 3 Total time 18

Note: There is looping in the above solution. Hence, it is not a unique solution to the travelling salesman problem. Hence, requires further modification.

(4) Modified Matrix - 1

A B C D a - 1 1 0 b 1 - 0 0 c 1 0 - 1 d 0 0 4 -

(5) Calculation of Minimum Total Time Required to complete the journey.

From To Journey Time a D 3 b C 6 c A 7 d B 3 Total time 19

The unique and optimum solution shows that the minimum time required is 19 hours.

Task For a salesman who has to visit n cities, which of the following are the ways of his tour plan

a. n! b. (n+1)!

c. (n-1)! d. n

• Multiple Choice

Course : Operations Research (MS-51)

University : indira gandhi national open university, this is a preview.

Access to all documents

Get Unlimited Downloads

Improve your grades

Get 30 days of free Premium

Share your documents to unlock

Why is this page out of focus?