Dec 15, 2024 · The Genetic Algorithm (GA) is an optimization technique inspired by Charles Darwin's theory of evolution through natural selection. First developed by John H. Holland in 1973 [2] , GA simulates biological processes such as selection, crossover, and mutation to explore and exploit solution spaces efficiently. ... Using Genetic Algorithms to Design Experiments: A Review C. Devon Lin Department of Mathematics and Statistics, Queen’s University Joint work with Christine M. Anderson-Cook, Michael S. Hamada, Lisa M. Moore, Randy R. Sitter Design and Analysis of Experiments (DAE) Oct 18, 2012 ... Dec 1, 2005 · Genetic algorithms (GAs) are a heuristic search and optimisation technique inspired by natural evolution. They have been successfully applied to a wide range of real-world problems of significant complexity. This paper is intended as an introduction to GAs aimed at immunologists and mathematicians interested in immunology. ... Jan 17, 2014 · Genetic algorithms (GAs) have been used in many disciplines to optimize solutions for a broad range of problems. In the last 20 years, the statistical literature has seen an increase in the use and study of this optimization algorithm for generating optimal designs in a diverse set of experimental settings. ... 208 GENETIC ALGORITHMS AND THE DESIGN OF EXPERIMENTS 1. Introduction. l,From their introduction by Holland [3] and pop­ ularization by Goldberg [4], most accounts of genetic algorithms (GAs) explain their behaviour by making reference to the biological metaphor of evolutionary adaptation. While this is helpful in providing an understand­ ... Mar 1, 2015 · It is concluded that the current GA implementations can, but do not always, provide a competitive methodology to produce substantial gains over standard optimal design strategies. Genetic algorithms (GAs) have been used in many disciplines to optimize solutions for a broad range of problems. In the last 20 years, the statistical literature has seen an increase in the use and study of this ... ... The genetic algorithm (GA) has most often been viewed from a biological perspective. The metaphors of natural selection, cross-breeding and mutation have been helpful in providing a framework in which to explain how and why they work. However, most practical... ... Jan 11, 1998 · The genetic algorithm (GA) has most often been viewed from a biological perspective. The metaphors of natural selection, cross-breeding and mutation have been helpful in providing a framework in ... ... It is simple to see that the exact model for the infinite population genetic algorithm has the same structure as the model on which the schema theorem is based. For example, if we accept that the string of all zeros (denoted here simply by the integer 0) is a special case of a hyperplane, then when H = 0, the following equivalence holds: ... Oct 6, 2024 · We chose this function to experiment with different genetic algorithm variations, such as activation functions (ReLU, Sigmoid, Softmax) and adaptive mutation rates. These adjustments are inspired by techniques in neural networks, where the goal is also optimization — minimizing the loss function to estimate weights. ... ">
phd

genetic algorithm model experiment

Genetic algorithm

Author: Yunchen Huo (yh2244), Ran Yi (ry357), Yanni Xie (yx682), Changlin Huang (ch2269), Jingyao Tong (jt887) (ChemE 6800 Fall 2024)

Stewards: Nathan Preuss, Wei-Han Chen, Tianqi Xiao, Guoqing Hu

  • 1 Introduction
  • 2 Algorithm Discussion
  • 3.1.1 1.1 Initialization (Generation 0)
  • 3.1.2.1 1.2.1 Evaluation
  • 3.1.2.2 1.2.2 Selection
  • 3.1.2.3 1.2.3 Crossover
  • 3.1.2.4 1.2.4 Mutation
  • 3.1.2.5 1.2.5 Insertion
  • 3.1.3.1 1.3.1 Evaluation
  • 3.1.3.2 1.3.2 Selection
  • 3.1.3.3 1.3.3 Crossover
  • 3.1.3.4 1.3.4 Mutation
  • 3.1.3.5 1.3.5 Insertion
  • 3.1.4 1.4 Conclusion
  • 3.2.1 2.1 Encoding the Variables
  • 3.2.2 2.2 Initialization
  • 3.2.3 Initial Population
  • 3.2.4 2.3 Evaluation
  • 3.2.5 2.4 Selection
  • 3.2.6 2.5 Crossover
  • 3.2.7 2.6 Mutation
  • 3.2.8 2.7 Insertion
  • 3.2.9 2.8 Repeat Steps 2.3-2.7
  • 4.1 Unsupervised Regression
  • 4.2 Virtual Power Plants
  • 4.3 Forecasting Financial Market Indices
  • 4.4 Software tools and platforms that utilize Genetic Algorithms
  • 5 Conclusion
  • 6 References

Introduction

The Genetic Algorithm (GA) is an optimization technique inspired by Charles Darwin's theory of evolution through natural selection [1] . First developed by John H. Holland in 1973 [2] , GA simulates biological processes such as selection, crossover, and mutation to explore and exploit solution spaces efficiently. Unlike traditional methods, GA does not rely on gradient information, making it particularly effective for solving complex, non-linear, and multi-modal problems.

GA operates on a population of candidate solutions, iteratively evolving toward better solutions by using fitness-based selection. This characteristic makes it suitable for tackling problems in various domains, such as engineering, machine learning, and finance. Its robustness and adaptability have established GA as a key technique in computational optimization and artificial intelligence research, as documented in Computational Optimization and Applications.

Algorithm Discussion

The GA was first introduced by John H. Holland [2] in 1973. It is an optimization technique based on Charles Darwin’s theory of evolution by natural selection.

genetic algorithm model experiment

Before diving into the algorithm, here are definitions of the basic terminologies.

  • Gene: The smallest unit that makes up the chromosome (decision variable)
  • Chromosome: A group of genes, where each chromosome represents a solution (potential solution)
  • Population: A group of chromosomes (a group of potential solutions)

GA involves the following seven steps:

  • Randomly generate the initial population for a predetermined population size
  • Evaluate the fitness of every chromosome in the population to see how good it is. Higher fitness implies better solution, making the chromosome more likely to be selected as a parent of next generation
  • Natural selection serves as the main inspiration of GA, where chromosomes are randomly selected from the entire population for mating, and chromosomes with higher fitness values are more likely to be selected [3] .
  • The purpose of crossover is to create superior offspring (better solutions) by combining parts from each selected parent chromosome. There are different types of crossover, such as single-point and double-point crossover [3] . In single-point crossover, the parent chromosomes are swapped before and after a single point. In double-point crossover, the parent chromosomes are swapped between two points [3] .
  • A mutation operator is applied to make random changes to the genes of children's chromosomes, maintaining the diversity of the individual chromosomes in the population and enabling GA to find better solutions [3] .
  • Insert the mutated children chromosomes back into the population
  • Maximum number of generations reached
  • No significant improvement from newer generations
  • Expected fitness value is achieved

Genetic Operators:

Steps 3-5 in GA involves techniques of changing the genes of chromosomes to create new generations. The functions that were applied to the populations are called genetic operators. The main types of GA operators include selection operator, crossover operator, and mutation operator. Below are some widely used operators:

  • Some famous selection operators include roulette wheel, rank, tournament, etc. Roulette wheel selection allocates strings onto a wheel based on their fitness value, then randomly selects solutions for the next generation [4] .
  • Single-point and double-point crossover operators were introduced in the algorithm above, and there is also a k-point crossover that selects multiple points and swaps the segments between those points of the parent chromosomes to generate new offspring [4] . Some other well-known crossover operators are uniform crossover, partially matched crossover, order crossover, and shuffle crossover [4] .
  • Mutation operator introduces variability into the population that helps the algorithm to find the global optimum. Displacement mutation operator randomly choose a substring from an individual and insert it into a new position [4] . Additionally, other prominent mutation operators are simple inversion mutation, scramble mutation, binary bit-flipping mutation, directed mutation, and others [5] .

Numerical Example

1. simple example.

{\displaystyle f(x)=x^{2}}

1.1 Initialization (Generation 0)

The initial population is randomly generated:

1.2 Generation 1

1.2.1 evaluation.

Calculate the fitness values:

1.2.2 Selection

Use roulette wheel selection to choose parents for crossover. Selection probabilities are calculated as:

{\displaystyle P({\text{Chromosome}})={\frac {\text{Fitness}}{\text{Total Fitness}}}.}

Compute the selection probabilities:

Cumulative probabilities:

Random numbers for selection:

{\displaystyle r_{1}=0.32,\quad r_{2}=0.60,\quad r_{3}=0.85,\quad r_{4}=0.10}

Selected parents:

  • Pair 1: 00111 and 11001
  • Pair 2: 11001 and 10010

1.2.3 Crossover

{\displaystyle P_{c}=0.7}

Pair 1: Crossover occurs at position 2.

{\displaystyle 00|111}

Pair 2: No crossover.

{\displaystyle 11001\ (x=25)}

1.2.4 Mutation

{\displaystyle P_{m}=0.1}

  • Mutations: Bit 1 and Bit 4 flip.

{\displaystyle 10011\ (x=19)}

  • Mutation: Bit 3 flips.

{\displaystyle 11011\ (x=27)}

  • Mutations: Bit 1 and Bit 5 flip.

{\displaystyle 01000\ (x=8)}

  • Mutations: Bit 1 and Bit 3 flip.

{\displaystyle 00110\ (x=6)}

1.2.5 Insertion

1.3 generation 2, 1.3.1 evaluation, 1.3.2 selection.

{\displaystyle {\text{Total Fitness}}=361+729+64+36=1,190}

Compute selection probabilities:

{\displaystyle r_{1}=0.20,\quad r_{2}=0.50,\quad r_{3}=0.80,\quad r_{4}=0.95}

  • Pair 1: 10011 and 11011
  • Pair 2: 11011 and 01000

1.3.3 Crossover

{\displaystyle 10|011}

Pair 2: Crossover occurs at position 4.

{\displaystyle 01|000}

1.3.4 Mutation

{\displaystyle {\text{Resulting Chromosome: }}10011}

1.3.5 Insertion

1.4 conclusion.

{\displaystyle f=729,\ x=27}

Due to the limitation of the page, we will not perform additional loops. In the following examples, we will show how to use code to perform multiple calculations on complex problems and specify stopping conditions.

2. Complex Example

We aim to maximize the function:

{\displaystyle f(x,y)=21.5+x\sin(4\pi x)+y\sin(20\pi y)}

subject to the constraints:

{\displaystyle -3.0\leq x\leq 12.1,\quad 4.1\leq y\leq 5.8.}

2.1 Encoding the Variables

{\displaystyle x}

2.2 Initialization

{\displaystyle {\text{Value}}={\text{Minimum}}+({\frac {\text{Binary Value}}{2^{\text{Bits}}-1}})\times {\text{Range}}.}

Initial Population

2.3 evaluation.

{\displaystyle f(x,y)}

2.4 Selection

Use roulette wheel selection to choose parents for crossover.

Total fitness:

{\displaystyle {\text{Total Fitness}}=19.35+22.65+30.12+16.40+28.75+21.10=138.37}

Selection probabilities are calculated as:

Selected pairs for crossover:

  • Pair 1: Chromosome 3 and Chromosome 5
  • Pair 2: Chromosome 2 and Chromosome 6
  • Pair 3: Chromosome 1 and Chromosome 4

2.5 Crossover

{\displaystyle 11100001\ 01011100}

Repeat for other pairs.

2.6 Mutation

{\displaystyle {\text{Original }}x:11100001\quad \longrightarrow \quad {\text{Mutated }}x:11101001.}

The new child becomes:

{\displaystyle {\text{Child 1: 11101001 01100110.}}}

2.7 Insertion

Evaluate the fitness of offspring and combine with the current population. Select the top 6 chromosomes to form the next generation.

2.8 Repeat Steps 2.3-2.7

Using the code ( https://github.com/AcidHCL/CornellWiki ) to perform the repeating process for 50 more generations we got

Fig.2. 50 iteration results

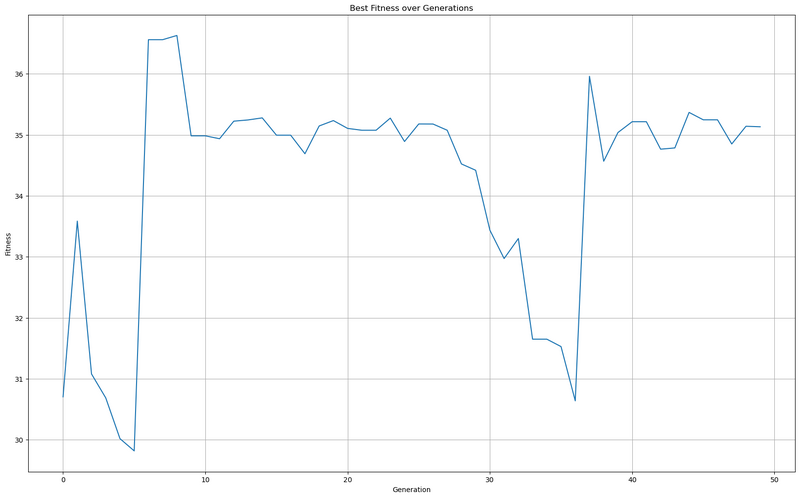
Fig.2. 50 iteration results

Based on Fig. 2 we can find the optimal value to be 35.2769.

Application

GA is one of the most important and successful algorithms in optimization, which can be demonstrated by numerous applications. Applications of GA include machine learning, engineering, finance and other domain applications, the following introduces the applications of GA in Unsupervised Regression, Virtual Power Plans and Forecasting Financial Market Indices.

Unsupervised Regression

The Unsupervised regression is a promising dimensionality reduction method [6] . The concept of the Unsupervised regression is to map from low-dimensional space into the high-dimensional space by using a regression model [7] . The goal of the Unsupervised Regression is to minimize the data space reconstruction error [6] . Common optimization methods to achieve this goal are the Nearest neighbor regression and the Kernel regression [6] . Since the mapping from the low-dimensional space into the high-dimensional space is usually complex, the data space reconstruction error function may become a non-convex multimodal function with multiple local optimal solutions. In this case, using GA can overcome local optima because of the population search, selection, crossover and mutation.

Virtual Power Plants

The renewable energy resources, such as wind power and solar power, have a distinct fluctuating character [6] . To address the inconvenience of such fluctuations on the power grid, engineers have introduced the concept of virtual power plants, which bundles various different power sources into a single unit that meets specific properties [6] .

The optimization goal is to minimize the absolute value of power in the virtual power plants system with a rule base [6] . This rule base is also known as the learning classifier system, which allows energy storage devices and standby power plants in the system to respond flexibly in different system states and achieve a balance between power consumption and generation [6] .

Since the rule base has complexity and a high degree of uncertainty, using GA can observably evolve the action part of the rule base. For example, in the complex energy scheduling process, GA can optimize the charge/discharge strategy of the energy storage equipment and the plan of start/stop of standby power plants to ensure the balance of power consumption and generation.

Forecasting Financial Market Indices

A financial market index consists of a weighted average of the prices of individual shares that make up the market [8] . In financial markets, many traders and analysts believe that stock prices move in trends and repeat price patterns [8] . Under this premise, using Grammatical Evolution(GE) to forecast the financial market indices and enhance trading decisions is a good choice.

GE is a machine learning method based on the GA [8] . GE uses a biologically-inspired, genotype-phenotype mapping process, evolving computer program in any language [8] . Unlike encoding the solution within the genetic material in the GA, the GE includes a many-to-one mapping process, which shows the robustness [8] .

While using GE to forecast financial market indices, people need to import processed historical stock price data. GE will learn price patterns in this data and generate models which can predict future price movements. These models can help traders and analysts identify the trend of the financial market, such as upward and downward trends.

Software tools and platforms that utilize Genetic Algorithms

MATLAB : The Global Optimization Toolbox of MATLAB is widely used for engineering simulations and machine learning.

Python : The DEAP and PyGAD in Python provide an environment for research and AI model optimization.

OpenGA : The OpenGA is a free C++ GA library, which is open-source. The OpenGA provides developers with a flexible way to implement GA for solving a variety of optimization problems [9] .

The GA is a versatile optimization tool inspired by evolutionary principles, excelling in solving complex and non-linear problems across diverse fields. Its applications, ranging from energy management to financial forecasting, highlight its adaptability and effectiveness. As computational capabilities advance, GA is poised to solve increasingly sophisticated challenges, reinforcing its relevance in both research and practical domains.

  • ↑ Lambora, A., Gupta, K., & Chopra, K. (2019). Genetic Algorithm - A Literature Review. 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, pp. 380–384.
  • ↑ 2.0 2.1 Holland, J. H. (1973). Genetic algorithms and the optimal allocation of trials. SIAM Journal on Computing, 2(2), 88–105
  • ↑ 3.0 3.1 3.2 3.3 Mirjalili, S. (2018). Genetic Algorithm. Evolutionary Algorithms and Neural Networks, Springer, pp. 43–56
  • ↑ 4.0 4.1 4.2 4.3 Katoch, S., Chauhan, S.S. & Kumar, V. (2021). A review on genetic algorithm: past, present, and future. Multimed Tools Appl 80, 8091–8126
  • ↑ Lim, S. M., Sultan, A. B. M., Sulaiman, M. N., Mustapha, A., & Leong, K. Y. (2017). Crossover and mutation operators of genetic algorithms. International journal of machine learning and computing, 7(1), 9-12
  • ↑ 6.0 6.1 6.2 6.3 6.4 6.5 6.6 Kramer, O. (2017). Studies in Computational Intelligence 679 Genetic Algorithm Essentials .
  • ↑ Kramer, O. (2016). Dimensionality reduction with unsupervised nearest neighbors .
  • ↑ 8.0 8.1 8.2 8.3 8.4 Chen, S.-H. (2012). Genetic Algorithms and Genetic Programming in Computational Finance . Springer Science & Business Media.
  • ↑ Arash-codedev. (2019, September 18). Arash-codedev/openGA . GitHub. https://github.com/Arash-codedev/openGA

Navigation menu

Genetic Algorithms — A Survey of Models and Methods

  • Reference work entry
  • Cite this reference work entry

genetic algorithm model experiment

  • Darrell Whitley 5 &
  • Andrew M. Sutton 6  

11k Accesses

26 Citations

This chapter first reviews the simple genetic algorithm. Mathematical models of the genetic algorithm are also reviewed, including the schema theorem, exact infinite population models, and exact Markov models for finite populations. The use of bit representations, including Gray encodings and binary encodings, is discussed. Selection, including roulette wheel selection, rank-based selection, and tournament selection, is also described. This chapter then reviews other forms of genetic algorithms, including the steady-state Genitor algorithm and the CHC (cross-generational elitist selection, heterogenous recombination, and cataclysmic mutation) algorithm. Finally, landscape structures that can cause genetic algorithms to fail are looked at, and an application of genetic algorithms in the domain of resource scheduling, where genetic algorithms have been highly successful, is also presented.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
  • Available as EPUB and PDF
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

genetic algorithm model experiment

Next Generation Genetic Algorithms: A User’s Guide and Tutorial

genetic algorithm model experiment

Genetic Algorithms

genetic algorithm model experiment

Genetic Algorithms and Applications

Bäck T (1996) Evolutionary algorithms in theory and practice. Oxford University Press, Oxford

MATH   Google Scholar  

Baker J (1987) Reducing bias and inefficiency in the selection algorithm. In: Grefenstette J (ed) GAs and their applications: 2nd international conference, Erlbaum, Hilsdale, NJ, pp 14–21

Google Scholar  

Bitner JR, Ehrlich G, Reingold EM (1976) Efficient generation of the binary reflected gray code and its applications. Commun ACM 19(9):517–521

Article   MathSciNet   MATH   Google Scholar  

Brent R (1973) Algorithms for minization with derivatives. Dover, Mineola, NY

Bridges C, Goldberg D (1987) An analysis of reproduction and crossover in a binary coded genetic algorithm. In: Grefenstette J (ed) GAs and their applications: 2nd international conference, Erlbaum, Cambridge, MA

Davis L (1985a) Applying adaptive algorithms to epistatic domains. In: Proceedings of the IJCAI-85, Los Angeles, CA

Davis L (1985b) Job shop scheduling with genetic algorithms. In: Grefenstette J (ed) International conference on GAs and their applications. Pittsburgh, PA, pp 136–140

Davis L (1991) Handbook of genetic algorithms. Van Nostrand Reinhold, New York

DeJong K (1993) Genetic algorithms are NOT function optimizers. In: Whitley LD (ed) FOGA – 2, Morgan Kaufmann, Los Altos, CA, pp 5–17

Eshelman L (1991) The CHC adaptive search algorithm: how to have safe search when engaging in nontraditional genetic recombination. In: Rawlins G (ed) FOGA – 1, Morgan Kaufmann, Los Altos, CA, pp 265–283

Eshelman L, Schaffer D (1991) Preventing premature convergence in genetic algorithms by preventing incest. In: Booker L, Belew R (eds) Proceedings of the 4th international conference on GAs. Morgan Kaufmann, San Diego, CA

Goldberg D (1987) Simple genetic algorithms and the minimal, deceptive problem. In: Davis L (ed) Genetic algorithms and simulated annealing. Pitman/Morgan Kaufmann, London, UK, chap 6

Goldberg D (1989a) Genetic algorithms and Walsh functions: Part II, deception and its analysis. Complex Syst 3:153–171

Goldberg D (1989b) Genetic algorithms in search, optimization and machine learning. Addison-Wesley, Reading, MA

Goldberg D (1990) A note on Boltzmann tournament selection for genetic algorithms and population-oriented simulated annealing. Tech. Rep. Nb. 90003. Department of Engineering Mechanics, University of Alabama, Tuscaloosa, AL

Goldberg D, Deb K (1991) A comparative analysis of selection schemes used in genetic algorithms. In: Rawlins G (ed) FOGA – 1, Morgan Kaufmann, San Mateo, CA, pp 69–93

Goldberg D, Lingle R (1985) Alleles, loci, and the traveling salesman problem. In: Grefenstette J (ed) International conference on GAs and their applications. London, UK, pp 154–159

Grefenstette J (1993) Deception considered harmful. In: Whitley LD (ed) FOGA – 2, Morgan Kaufmann, Vail, CO, pp 75–91

Hansen N (2006) The CMA evolution strategy: a comparing review. In: Toward a new evolutionary computation: advances on estimation of distribution algorithms. Springer, Heidelberg, Germany, pp 75–102

Hansen N (2008) Adaptive encoding: how to render search coordinate system invariant. In: Proceedings of 10th international conference on parallel problem solving from nature. Springer, Dortmund, Germany, pp 205–214

Heckendorn R, Rana S, Whitley D (1999a) Polynomial time summary statistics for a generalization of MAXSAT. In: GECCO-99, Morgan Kaufmann, San Francisco, CA, pp 281–288

Heckendorn R, Rana S, Whitley D (1999b) Test function generators as embedded landscapes. In: Foundations of genetic algorithms FOGA – 5, Morgan Kaufmann, Los Atlos, CA

Heckendorn RB, Whitley LD, Rana S (1996) Nonlinearity, Walsh coefficients, hyperplane ranking and the simple genetic algorithm. In: FOGA – 4, San Diego, CA

Ho Y (1994) Heuristics, rules of thumb, and the 80/20 proposition. IEEE Trans Automat Cont 39(5):1025–1027

Article   Google Scholar  

Ho Y, Sreenivas RS, Vakili P (1992) Ordinal optimization of discrete event dynamic systems. Discrete Event Dyn Syst 2(1):1573–7594

Holland J (1975) Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor, MI

Holland JH (1992) Adaptation in natural and artificial systems, 2nd edn. MIT Press, Cambridge, MA

Schaffer JD, Eshelman L (1993) Real-coded genetic algorithms and interval schemata. In: Whitley LD (ed) FOGA – 2, Morgan Kaufmann, Los Atlos, CA

Mathias KE, Whitley LD (1994) Changing representations during search: a comparative study of delta coding. J Evolut Comput 2(3):249–278

Nagata Y, Kobayashi S (1997) Edge assembly crossover: a high-power genetic algorithm for the traveling salesman problem. In: Bäck T (ed) Proceedings of the 7th international conference on GAs, Morgan Kaufmann, California, pp 450–457

Nix A, Vose M (1992) Modelling genetic algorithms with Markov chains. Ann Math Artif Intell 5:79–88

Poli R (2005) Tournament selection, iterated coupon-collection problem, and backward-chaining evolutionary algorithms. In: Foundations of genetic algorithms, Springer, Berlin, Germany, pp 132–155

Chapter   Google Scholar  

Radcliffe N, Surry P (1995) Fundamental limitations on search algorithms: evolutionary computing in perspective. In: van Leeuwen J (ed) Lecture notes in computer science, vol 1000, Springer, Berlin, Germany

Rana S, Whitley D (1997) Representations, search and local optima. In: Proceedings of the 14th national conference on artificial intelligence AAAI-97. MIT Press, Cambridge, MA, pp 497–502

Rana S, Heckendorn R, Whitley D (1998) A tractable Walsh analysis of SAT and its implications for genetic algorithms. In: AAAI98, MIT Press, Cambridge, MA, pp 392–397

Rosenbrock H (1960) An automatic method for finding the greatest or least value of a function. Comput J 3:175–184

Article   MathSciNet   Google Scholar  

Salomon R (1960) Reevaluating genetic algorithm performance under coordinate rotation of benchmark functions. Biosystems 39(3):263–278

Schaffer JD (1987) Some effects of selection procedures on hyperplane sampling by genetic algorithms. In: Davis L (ed) Genetic algorithms and simulated annealing. Morgan Kaufmann, San Francisco, CA, pp 89–130

Schwefel HP (1981) Numerical optimization of computer models. Wiley, New York

Schwefel HP (1995) Evolution and optimum seeking. Wiley, New York

Sokolov A, Whitley D (2005) Unbiased tournament selection. In: Proceedings of the 7th genetic and evolutionary computation conference. The Netherlands, pp 1131–1138

Spears W, Jong KD (1991) An analysis of multi-point crossover. In: Rawlins G (ed) FOGA – 1, Morgan Kaufmann, Los Altos, CA, pp 301–315

Starkweather T, Whitley LD, Mathias KE (1990) Optimization using distributed genetic algorithms. In: Schwefel H, Männer R (eds) Parallel problem solving from nature. Springer, London, UK, pp 176–185

Starkweather T, McDaniel S, Mathias K, Whitley D, Whitley C (1991) A comparison of genetic sequencing operators. In: Booker L, Belew R (eds) Proceedings of the 4th international conference on GAs. Morgan Kaufmann, San Mateo, CA, pp 69–76

Suh J, Gucht DV (1987) Distributed genetic algorithms. Tech. rep., Indiana University, Bloomington, IN

Syswerda G (1989) Uniform crossover in genetic algorithms. In: Schaffer JD (ed) Proceedings of the 3rd international conference on GAs, Morgan Kaufmann, San Mateo, CA

Syswerda G (1991) Schedule optimization using genetic algorithms. In: Davis L (ed) Handbook of genetic algorithms, Van Nostrand Reinhold, New York, chap 21

Syswerda G, Palmucci J (1991) The application of genetic algorithms to resource scheduling. In: Booker L, Belew R (eds) Proceedings of the 4th international conference on GAs, Morgan Kaufmann, San Mateo, CA

Vose M (1993) Modeling simple genetic algorithms. In: Whitley LD (ed) FOGA – 2, Morgan Kaufmann, San Mateo, CA, pp 63–73

Vose M (1999) The simple genetic algorithm. MIT Press, Cambridge, MA

Vose M, Liepins G (1991) Punctuated equilibria in genetic search. Complex Syst 5:31–44

MathSciNet   MATH   Google Scholar  

Vose M, Wright A (1997) Simple genetic algorithms with linear fitness. Evolut Comput 2(4):347–368

Watson JP, Rana S, Whitley D, Howe A (1999) The impact of approximate evaluation on the performance of search algorithms for warehouse scheduling. J Scheduling 2(2):79–98

Whitley D (1999) A free lunch proof for gray versus binary encodings. In: GECCO-99, Morgan Kaufmann, Orlando, FL, pp 726–733

Whitley D, Kauth J (1988) GENITOR: A different genetic algorithm. In: Proceedings of the 1988 Rocky Mountain conference on artificial intelligence, Denver, CO

Whitley D, Rowe J (2008) Focused no free lunch theorems. In: GECCO-08, ACM Press, New York

Whitley D, Yoo NW (1995) Modeling permutation encodings in simple genetic algorithm. In: Whitley D, Vose M (eds) FOGA – 3, Morgan Kaufmann, San Mateo, CA

Whitley D, Starkweather T, Fuquay D (1989) Scheduling problems and traveling salesmen: the genetic edge recombination operator. In: Schaffer JD (ed) Proceedings of the 3rd international conference on GAs. Morgan Kaufmann, San Francisco, CA

Whitley D, Das R, Crabb C (1992) Tracking primary hyperplane competitors during genetic search. Ann Math Artif Intell 6:367–388

Article   MATH   Google Scholar  

Whitley D, Beveridge R, Mathias K, Graves C (1995a) Test driving three 1995 genetic algorithms. J Heuristics 1:77–104

Whitley D, Mathias K, Pyeatt L (1995b) Hyperplane ranking in simple genetic algorithms. In: Eshelman L (ed) Proceedings of the 6th international conference on GAs. Morgan Kaufmann, San Francisco, CA

Whitley D, Mathias K, Rana S, Dzubera J (1996) Evaluating evolutionary algorithms. Artif Intell J 85:1–32

Whitley LD (1989) The GENITOR algorithm and selective pressure: why rank based allocation of reproductive trials is best. In: Schaffer JD (ed) Proceedings of the 3rd international conference on GAs. Morgan Kaufmann, San Francisco, CA, pp 116–121

Whitley LD (1991) Fundamental principles of deception in genetic search. In: Rawlins G (ed) FOGA – 1, Morgan Kaufmann, San Francisco, CA, pp 221–241

Whitley LD (1993) An executable model of the simple genetic algorithm. In: Whitley LD (ed) FOGA – 2, Morgan Kaufmann, Vail, CO, pp 45–62

Wolpert DH, Macready WG (1995) No free lunch theorems for search. Tech. Rep. SFI-TR-95-02-010, Santa Fe Institute, Santa Fe, NM

Download references

Acknowledgments

This research was partially supported by a grant from the Air Force Office of Scientific Research, Air Force Materiel Command, USAF, under grant number FA9550-08-1-0422. The U.S. Government is authorized to reproduce and distribute reprints for Governmental purposes, notwithstanding any copyright notation thereon. Funding was also provided by the Coors Brewing Company, Golden, Colorado.

Author information

Authors and affiliations.

Department of Computer Science, Colorado State University, Fort Collins, CO, USA

Darrell Whitley

Andrew M. Sutton

You can also search for this author in PubMed   Google Scholar

Editor information

Editors and affiliations.

LIACS, Leiden University, Leiden, The Netherlands

Grzegorz Rozenberg

Computer Science Department, University of Colorado, Boulder, USA

Thomas Bäck

Joost N. Kok

Rights and permissions

Reprints and permissions

Copyright information

© 2012 Springer-Verlag Berlin Heidelberg

About this entry

Cite this entry.

Whitley, D., Sutton, A.M. (2012). Genetic Algorithms — A Survey of Models and Methods. In: Rozenberg, G., Bäck, T., Kok, J.N. (eds) Handbook of Natural Computing. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-92910-9_21

Download citation

DOI : https://doi.org/10.1007/978-3-540-92910-9_21

Publisher Name : Springer, Berlin, Heidelberg

Print ISBN : 978-3-540-92909-3

Online ISBN : 978-3-540-92910-9

eBook Packages : Computer Science Reference Module Computer Science and Engineering

Share this entry

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

  • Publish with us

Policies and ethics

  • Find a journal
  • Track your research

IMAGES

  1. The Basic Genetic Algorithm: flowchart.

    genetic algorithm model experiment

  2. A Review on Genetic Algorithm and Its Applications in Data Mining

    genetic algorithm model experiment

  3. Illustration of the genetic algorithm concept, showing an example...

    genetic algorithm model experiment

  4. Genetic Algorithms: Components & Applications

    genetic algorithm model experiment

  5. Genetic Algorithm Applications in Machine Learning

    genetic algorithm model experiment

  6. PPT

    genetic algorithm model experiment

COMMENTS

  1. Genetic algorithm - Cornell University Computational ...

    Dec 15, 2024 · The Genetic Algorithm (GA) is an optimization technique inspired by Charles Darwin's theory of evolution through natural selection. First developed by John H. Holland in 1973 [2] , GA simulates biological processes such as selection, crossover, and mutation to explore and exploit solution spaces efficiently.

  2. Using Genetic Algorithms to Design Experiments: A Review

    Using Genetic Algorithms to Design Experiments: A Review C. Devon Lin Department of Mathematics and Statistics, Queen’s University Joint work with Christine M. Anderson-Cook, Michael S. Hamada, Lisa M. Moore, Randy R. Sitter Design and Analysis of Experiments (DAE) Oct 18, 2012

  3. Genetic algorithms for modelling and optimisation - ScienceDirect

    Dec 1, 2005 · Genetic algorithms (GAs) are a heuristic search and optimisation technique inspired by natural evolution. They have been successfully applied to a wide range of real-world problems of significant complexity. This paper is intended as an introduction to GAs aimed at immunologists and mathematicians interested in immunology.

  4. Using Genetic Algorithms to Design Experiments: A Review

    Jan 17, 2014 · Genetic algorithms (GAs) have been used in many disciplines to optimize solutions for a broad range of problems. In the last 20 years, the statistical literature has seen an increase in the use and study of this optimization algorithm for generating optimal designs in a diverse set of experimental settings.

  5. GENETIC ALGORITHMS AND THE DESIGN OF EXPERIMENTS - Springer

    208 GENETIC ALGORITHMS AND THE DESIGN OF EXPERIMENTS 1. Introduction. l,From their introduction by Holland [3] and pop­ ularization by Goldberg [4], most accounts of genetic algorithms (GAs) explain their behaviour by making reference to the biological metaphor of evolutionary adaptation. While this is helpful in providing an understand­

  6. Using Genetic Algorithms to Design Experiments: A Review

    Mar 1, 2015 · It is concluded that the current GA implementations can, but do not always, provide a competitive methodology to produce substantial gains over standard optimal design strategies. Genetic algorithms (GAs) have been used in many disciplines to optimize solutions for a broad range of problems. In the last 20 years, the statistical literature has seen an increase in the use and study of this ...

  7. Genetic Algorithms and the Design of Experiments

    The genetic algorithm (GA) has most often been viewed from a biological perspective. The metaphors of natural selection, cross-breeding and mutation have been helpful in providing a framework in which to explain how and why they work. However, most practical...

  8. Genetic Algorithms and The Design of Experiments - ResearchGate

    Jan 11, 1998 · The genetic algorithm (GA) has most often been viewed from a biological perspective. The metaphors of natural selection, cross-breeding and mutation have been helpful in providing a framework in ...

  9. Genetic Algorithms — A Survey of Models and Methods - Springer

    It is simple to see that the exact model for the infinite population genetic algorithm has the same structure as the model on which the schema theorem is based. For example, if we accept that the string of all zeros (denoted here simply by the integer 0) is a special case of a hyperplane, then when H = 0, the following equivalence holds:

  10. Advancing Genetic Algorithms and Their Applications

    Oct 6, 2024 · We chose this function to experiment with different genetic algorithm variations, such as activation functions (ReLU, Sigmoid, Softmax) and adaptive mutation rates. These adjustments are inspired by techniques in neural networks, where the goal is also optimization — minimizing the loss function to estimate weights.