problem solving linear equations in two variables

Linear Equations in Two Variables

A linear equation in two variables is an equation in which two variables have the exponent 1. A system of equations with two variables has a unique solution, no solutions, or infinitely many solutions. A linear system of equations may have 'n' number of variables. An important thing to keep in mind while solving linear equations with n number of variables is that there must be n equations to solve and determine the value of variables.

Linear equations in two variables are the algebraic equations which are of the form (or can be converted to the form) y = mx + b, where m is the slope and b is the y-intercept . They are the equations of the first order. For example, y = 2x + 3 and 2y = 4x + 9 are two-variable linear equations.

What are Linear Equations in Two Variables?

The linear equations in two variables are the equations in which each of the two variables is of the highest order ( exponent ) of 1 and may have one, none, or infinitely many solutions. The standard form of a two-variable linear equation is ax + by + c = 0 where x and y are the two variables. The solutions can also be written in ordered pairs like (x, y). The graphical representation of the pairs of linear equations in two variables includes two straight lines which could be:

• intersecting lines
• parallel lines or
• coincident lines .

Forms of Linear Equations in Two Variables

A linear equation in two variables can be in different forms like standard form , intercept form and point-slope form . For example, the same equation 2x + 3y=9 can be represented in each of the forms like 2x + 3y - 9=0 (standard form), y = (-2/3)x + 3 ( slope-intercept form ), and y - 5/3 = -2/3(x + (-2)) (point-slope form). Look at the image given below showing all these three forms of representing linear equations in two variables with examples.

The system of equations means the collection of equations and they are also referred to as simultaneous linear equations . We will learn how to solve pair of linear equations in two variables using different methods.

Solving Pairs of Linear Equations in Two Variables

There are five methods to solve pairs of linear equations in two variables as shown below:

• Graphical Method
• Substitution Method
• Cross Multiplication Method
• Elimination Method

Determinant Method

Graphical method for solving linear equations in two variables.

The steps to solve linear equations in two variables graphically are given below:

• Step 1 : To solve a system of two equations in two variables graphically , we graph each equation. To know how, click here or follow steps 2 and 3 below.
• Step 2 : To graph an equation manually, first convert it to the form y = mx+b by solving the equation for y.
• Step 3 : Start putting the values of x as 0, 1, 2, and so on and find the corresponding values of y, or vice-versa.
• Step 4 : Identify the point where both lines meet.
• Step 5 : The point of intersection is the solution of the given system.

Example: Find the solution of the following system of equations graphically.

Solution: We will graph them and see whether they intersect at a point. As you can see below, both lines meet at (1, 2). Thus, the solution of the given system of linear equations is x=1 and y=2.

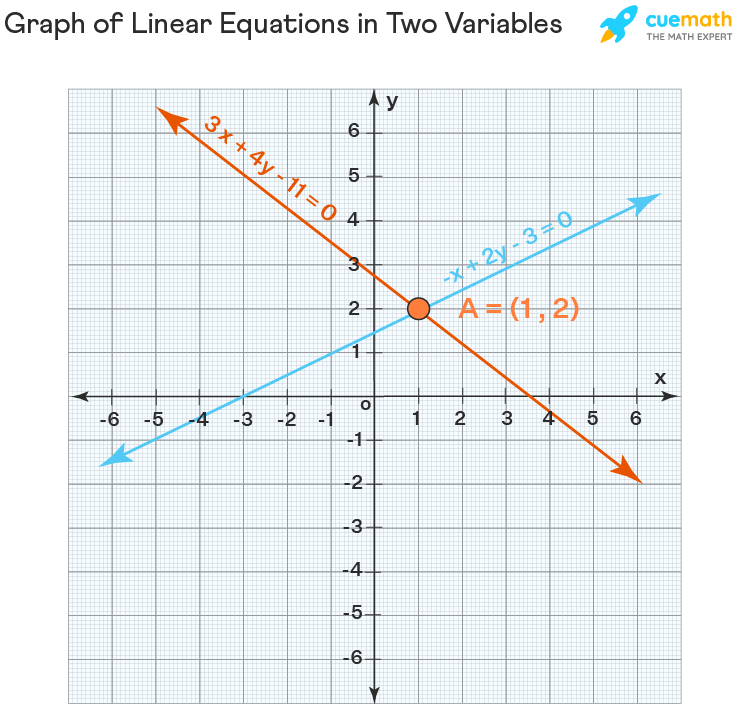
But both lines may not intersect always. Sometimes they may be parallel. In that case, the pairs of linear equations in two variables have no solution. In some other cases, both lines coincide with each other. In that case, each point on that line is a solution of the given system and hence the given system has an infinite number of solutions.

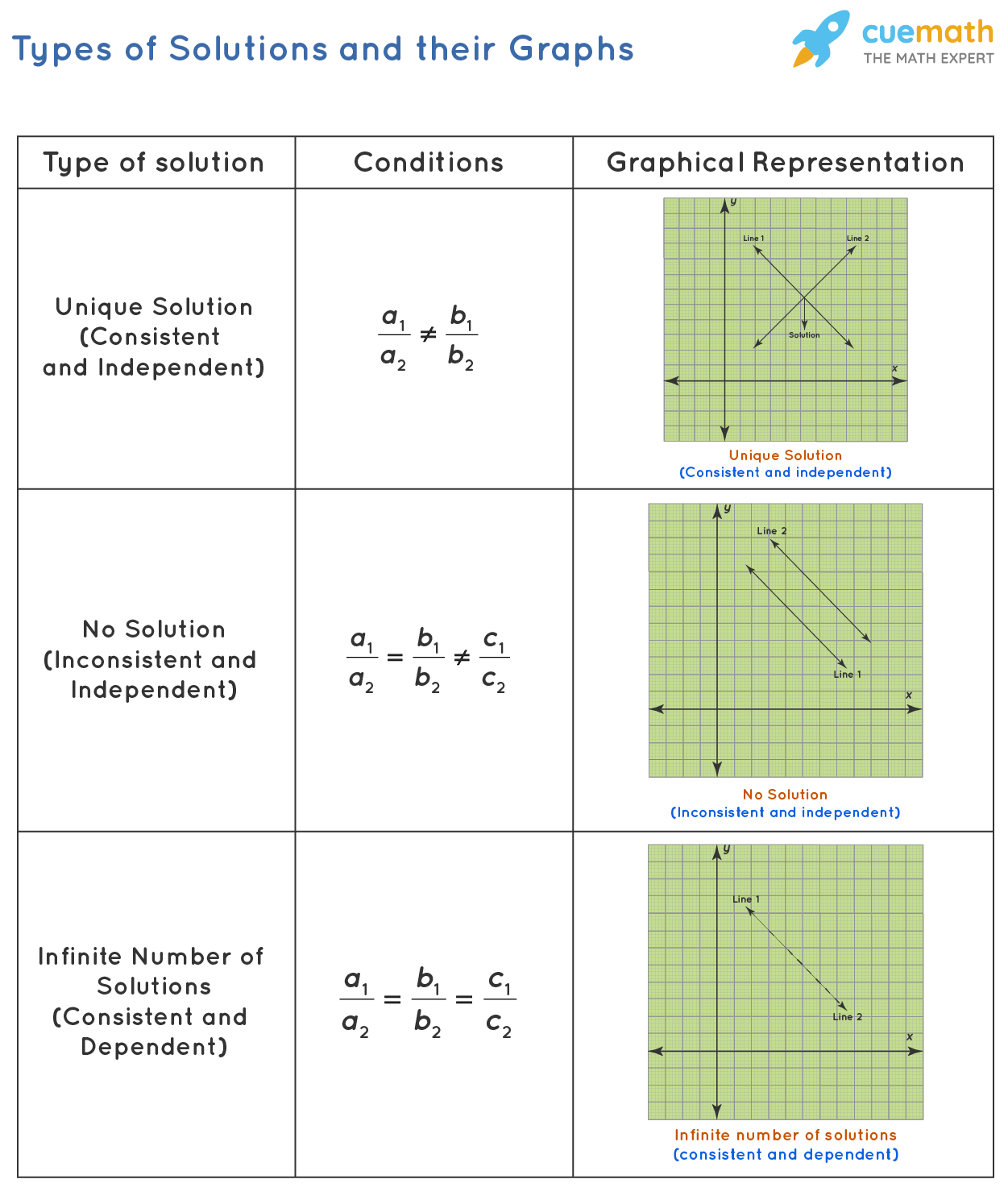
Consistent and Inconsistent System of Linear Equations:

• If the system has a solution, then it is said to be consistent;
• otherwise, it is said to be inconsistent.

Independent and Dependent System of Linear Equations:

• If the system has a unique solution, then it is independent.
• If it has an infinite number of solutions, then it is dependent. It means that one variable depends on the other.

Consider a system of two linear equations: a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0. Here we can understand when a linear system with two variables is consistent/inconsistent and independent/dependent.

Method of Substitution

To solve a system of two linear equations in two variables using the substitution method , we have to use the steps given below:

• Step 1: Solve one of the equations for one variable.
• Step 2: Substitute this in the other equation to get an equation in terms of a single variable.
• Step 3: Solve it for the variable.
• Step 4: Substitute it in any of the equations to get the value of another variable.

Example: Solve the following system of equations using the substitution method. x+2y-7=0 2x-5y+13=0

Solution: Let us solve the equation, x+2y-7=0 for y: x+2y-7=0 ⇒2y=7-x ⇒ y=(7-x)/2

Substitute this in the equation, 2x-5y+13=0:

2x-5y+13=0 ⇒ 2x-5((7-x)/2)+13=0 ⇒ 2x-(35/2)+(5x/2)+13=0 ⇒ 2x + (5x/2) = 35/2 - 13 ⇒ 9x/2 = 9/2 ⇒ x=1

Substitute x=1 this in the equation y=(7-x)/2:

y=(7-1)/2 = 3

Therefore, the solution of the given system is x=1 and y=3.

Consider a system of linear equations: a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0.

To solve this using the cross multiplication method , we first write the coefficients of each of x and y and constants as follows:

Here, the arrows indicate that those coefficients have to be multiplied. Now we write the following equation by cross-multiplying and subtracting the products. \(\dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}=\dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}}\)

From this equation, we get two equations:

\(\begin{align} \dfrac{x}{b_{1} c_{2}-b_{2} c_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}} \\[0.2cm] \dfrac{y}{c_{1} a_{2}-c_{2} a_{1}}&=\dfrac{1}{a_{1} b_{2}-a_{2} b_{1}} \end{align}\)

Solving each of these for x and y, the solution of the given system is:

\(\begin{align} x&=\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\\[0.2cm] y&=\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}} \end{align}\)

Method of Elimination

To solve a system of linear equations in two variables using the elimination method , we will use the steps given below:

• Step 1: Arrange the equations in the standard form: ax+by+c=0 or ax+by=c.
• Step 2: Check if adding or subtracting the equations would result in the cancellation of a variable.
• Step 3: If not, multiply one or both equations by either the coefficient of x or y such that their addition or subtraction would result in the cancellation of any one of the variables.
• Step 4: Solve the resulting single variable equation.
• Step 5: Substitute it in any of the given equations to get the value of another variable.

Example: Solve the following system of equations using the elimination method. 2x+3y-11=0 3x+2y-9=0

Adding or subtracting these two equations would not result in the cancellation of any variable. Let us aim at the cancellation of x. The coefficients of x in both equations are 2 and 3. Their LCM is 6. We will make the coefficients of x in both equations 6 and -6 such that the x terms get canceled when we add the equations.

3 × (2x+3y-11=0) ⇒ 6x+9y-33=0 -2 × (3x+2y-9=0) ⇒ -6x-4y+18=0

Now we will add these two equations: 6x+9y-33=0 -6x-4y+18=0

On adding both the above equations we get, ⇒ 5y-15=0 ⇒ 5y=15 ⇒ y=3

Substitute this in one of the given two equations and solve the resultant variable for x. 2x+3y-11=0 ⇒ 2x+3(3)-11=0 ⇒ 2x+9-11=0 ⇒ 2x=2 ⇒ x=1

Therefore, the solution of the given system of equations is x=1 and y=3.

The determinant of a 2 × 2 matrix is obtained by cross-multiplying elements starting from the top left corner and subtracting the products.

Consider a system of linear equations in two variables: a 1 x + b 1 y = c 1 and a 2 x + b 2 y = c 2 . To solve them using the determinants method (which is also known as Crammer's Rule ), follow the steps given below:

• Step 1: We first find the determinant formed by the coefficients of x and y and label it Δ. Δ = \(\left|\begin{array}{ll}a_1 & b_1 \\a_2 & b_2\end{array}\right| = a_1 b_2 - a_2b_1\)
• Step 2: Then we find the determinant Δ x which is obtained by replacing the first column of Δ with constants. Δ x = \(\left|\begin{array}{ll}c_1 & b_1 \\c_2 & b_2\end{array}\right| = c_1 b_2 - c_2b_1\)
• Step 3: We then find the determinant Δ y which is obtained by replacing the second column of Δ with constants. Δ y = \(\left|\begin{array}{ll}a_1 & c_1 \\a_2 & c_2\end{array}\right| = a_1 c_2 - a_2c_1\)

Now, the solution of the given system of linear equations is obtained by the formulas:

• x = Δ x / Δ
• y = Δ y / Δ

Important Points on Linear Equations with Two Variables:

• A linear equation in two variables is of the form ax + by + c = 0, where x and y are variables; and a, b, and c are real numbers.
• A pair of linear equations are of the form a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0 and its solution is a pair of values (x, y) that satisfy both equations.
• To solve linear equations in two variables, we must have at least two equations.
• A linear equation in two variables has infinitely many solutions.

Tricks and Tips:

While solving the equations using either the substitution method or the elimination method:

• If we get an equation that is true (i.e., something like 0 = 0, -1 = -1, etc), then it means that the system has an infinite number of solutions.
• If we get an equation that is false (i.e., something like 0 = 2, 3 = -1, etc), then it means that the system has no solution.

☛Related Topics:

• Solving Linear Equations Calculator
• Equation Calculator
• System of Equations Calculator
• Linear Graph Calculator

Linear Equations in Two Variables Examples

Example 1: The sum of the digits of a two-digit number is 8. When the digits are reversed, the number is increased by 18. Find the number.

Solution: Let us assume that x and y are the tens digit and the ones digit of the required number. Then the number is 10x+y.

And the number when the digits are reversed is 10y+x.

The question says, "The sum of the digits of a two-digit number is 8".

So from this, we get a linear equation in two variables: x+y=8.

Also, when the digits are reversed, the number is increased by 18.

So, the equation is 10y+x =10x+y+18

⇒ 10(8-x)+x =10x+(8-x)+18 (by substituting the value of y) ⇒ 80-10x+x =10x+8-x+18 ⇒ 80-9x=9x+26 ⇒ 18x = 54 ⇒ x=3

Substituting x=3 in y=8-x, we get, ⇒ y = 8-3 = 5 ⇒ 10x+y=10(3)+5 =35 Answer: The required number is 35.

Example 2: Jake's piggy bank has 11 coins (only quarters or dimes) that have a total value of $1.85. How many dimes and quarters does the piggy bank has?

Solution: Let us assume that the number of dimes be x and the number of quarters be y in the piggy bank. Let us form linear equations in two variables based on the given information.

Since there are 11 coins in total, x+y=11 ⇒ y=11-x. We know that, 1 dime = 10 cents and 1 quarter = 25 cents. The total value of the money in the piggy bank is $1.85 (185 cents).

Thus we get the equation 10x + 25y = 185 ⇒ 10x + 25(11-x) = 185 (as y = 11-x) ⇒ 10x + 275 - 25x =185 ⇒ -15x +275 =185 ⇒ -15x=-90 ⇒ x = 6

Substitute this value of x in x+y=11. ⇒ y=11-6=5

Answer: Therefore, the number of dimes is 6 and the number of quarters is 5.

Example 3: In a river, a boat can travel 30 miles upstream in 2 hours. The same boat can travel 51 miles downstream in 3 hours. Find,

• What is the speed of the boat in still water?
• What is the speed of the current?

Solution: Let us assume that:

• the speed of the boat in still water = x miles per hour
• the speed of current = y miles per hour.

During upstream, the current pulls back the boat's speed and the speed of the boat upstream = (x-y). During downstream, the current's speed adds to the boat's speed and the speed of the boat downstream = (x+y).

Using the last two columns of the table, we can form a pair of linear equations in two variables: x-y=15 x+y=17

Adding both equations we get: 2x = 32 ⇒ x=16

Substitute x=16 in x+y=17 16+y= 17 y=1

Answer: Therefore, the speed of the boat is 16 miles per hour and the speed of the current is 1 mile per hour.

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Linear Equations in Two Variables

go to slide go to slide

FAQs on Linear Equations in Two Variables

What is meant by linear equation in two variables.

A linear equation is an equation with degree 1. A linear equation in two variables is a type of linear equation in which there are 2 variables present. For example, 2x - y = 45, x+y =35, a-b = 45 etc.

How do you Identify Linear Equations in Two Variables?

We can identify a linear equation in two variables if it can be expressed in the form ax+by+ c = 0, consisting of two variables x and y and the highest degree of the given equation is 1.

Can You Solve a Pair of Linear Equations in Two Variables?

Yes, we can solve pair of linear equations in two variables using different methods and ensure there are two equations present in the given system of equations so as to obtain the values of variables. If there is one solution it means that the given lines are intersecting, if there is no solution possible, then it means that the given equations are of parallel lines. If there are infinitely many solutions possible, it means that the given equations are forming coincidental lines.

How to Graphically Represent a Pair of Linear Equations in Two Variables?

We can represent linear equations in two variables graphically using the steps given below:

• Step 1: A system of two equations in two variables can be solved graphically by graphing each equation by converting it to the form y=mx+b by solving the equation for y.
• Step 2: The points where both lines meet are identified.
• Step 3: The point of intersection is the solution of the given pair of linear equations in two variables.

How Does One Solve the System of Linear Equations in Two Variables?

We have different methods to solve the system of linear equations:

• Determinant or Matrix Method

How Many Solutions Does a Linear Equation with Two Variables Have?

Suppose we have a 1 x + b 1 y + c 1 = 0 and a 2 x + b 2 y + c 2 = 0. The solutions of a linear equation with two variables are:

• One and unique if a 1 /a 2 ≠ b 1 /b 2
• None if a 1 /a 2 = b 1 /b 2 ≠ c 1 /c 2
• Infinitely many if a 1 /a 2 = b 1 /b 2 = c 1 /c 2

How is a Linear Inequality in Two Variables like a Linear Equation in Two Variables?

A linear inequality in two variables and a linear equation in two variables have the following things in common:

• The degree of a linear equation and linear inequality is always 1.
• Both of them can be solved graphically.
• The way to solve a linear inequality is the same as linear equations except that it is separated by an inequality symbol. But note that the inequality rules should be taken care of.

• Math Article

Linear Equations In Two Variables

Linear equations in two variables, explain the geometry of lines or the graph of two lines, plotted to solve the given equations. As we already know, the linear equation represents a straight line. The plotting of these graphs will help us to solve the equations, which consist of unknown variables. Previously we have learned to solve linear equations in one variable , here we will find the solutions for the equations having two variables.

An equation is said to be linear equation in two variables if it is written in the form of ax + by + c=0, where a, b & c are real numbers and the coefficients of x and y, i.e a and b respectively, are not equal to zero.

For example, 10x+4y = 3 and -x+5y = 2 are linear equations in two variables.

The solution for such an equation is a pair of values, one for x and one for y which further makes the two sides of an equation equal.

Also, read: 

• Linear Equations In Two Variables Class 9
• Solving Linear Equations
• Applications Of Linear Equations

Solution of Linear Equations in Two Variables

The solution of linear equations in two variables, ax+by = c, is a particular point in the graph, such that when x-coordinate is multiplied by a and y-coordinate is multiplied by b, then the sum of these two values will be equal to c. 

Basically, for linear equation in two variables, there are infinitely many solutions.

In order to find the solution of Linear equation in 2 variables, two equations should be known to us.

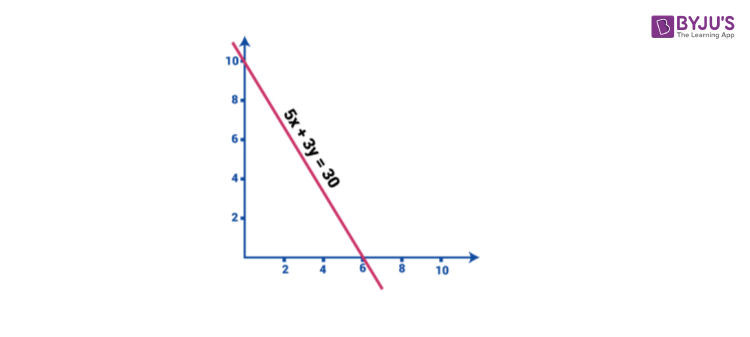
Consider for Example:

5x + 3y = 30

The above equation has two variables namely x and y.

Graphically this equation can be represented by substituting the variables to zero.

The value of x when y=0 is

5x + 3(0) = 30

and the value of y when x = 0 is,

5 (0) + 3y = 30

It is now understood that to solve linear equation in two variables, the two equations have to be known and then the substitution method can be followed. Let’s understand this with a few example questions.

Unique Solution

For the given linear equations in two variables, the solution will be unique for both the equations, if and only if they intersect at a single point. 

The condition to get the unique solution for the given linear equations is, the slope of the line formed by the two equations, respectively, should not be equal.

Consider, m 1 and m 2 are two slopes of equations of two lines in two variables. So, if the equations have a unique solution, then:

No Solution

If the two linear equations have equal slope value, then the equations will have no solutions.

This is because the lines are parallel to each other and do not intersect.

System of Linear Equations in Two Variables

Instead of finding the solution for a single linear equation in two variables, we can take two sets of linear equations, both having two variables in them and find the solutions. So, basically the system of linear equations is defined when there is more than one linear equation. 

For example, a+b = 15 and a-b = 5, are the system of linear equations in two variables. Because, the point a = 10 and b = 5 is the solution for both equations, such as:

a+b=10 + 5 = 15

a-b=10-5 = 5

Hence, proved point (10,5) is solution for both a+b=15 and a-b=5.

Problems and Solutions

Question: Find the value of variables which satisfies the following equation:

2x + 5y = 20 and 3x+6y =12.

Using the method of substitution to solve the pair of linear equation, we have:

2x + 5y = 20…………………….(i)

3x+6y =12……………………..(ii)

Multiplying equation (i) by 3 and (ii) by 2, we have:

6x + 15y = 60…………………….(iii)

6x+12y = 24……………………..(iv)

Subtracting equation (iv) from (iii)

Substituting the value of y in any of the equation (i) or (ii), we have

2x + 5(12) = 20

Therefore, x=-20 and y =12 is the point where the given equations intersect.

Now, it is important to know the situational examples which are also known as word problems from linear equations in 2 variables.

Check:  Linear Equations Calculator

Word Problems

Question 1:  A boat running downstream covers a distance of 20 km in 2 hours while for covering the same distance upstream, it takes 5 hours. What is the speed of the boat in still water?

These types of questions are the real-time examples of linear equations in two variables.

In water, the direction along the stream is called downstream. And, the direction against the stream is called upstream.

Let us consider the speed of a boat is u km/h and the speed of the stream is v km/h, then:

Speed Downstream = (u + v) km/h

Speed Upstream = (u – v) km/h

We know that, Speed = Distance/Time

So, the speed of boat when running downstream = (20⁄2) km/h = 10 km/h

The speed of boat when running upstream = (20⁄5) km/h = 4 km/h

From above, u + v = 10…….(1)

u – v = 4 ………. (2)

Adding equation 1 and 2, we get: 2u = 1

Also, v = 3 km/h

Therefore, the speed of the boat in still water = u = 7 km/h

Question 2: A boat running upstream takes 6 hours 30 minutes to cover a certain distance, while it takes 3 hours to cover the same distance running downstream. What is the ratio between the speed of the boat and speed of the water current, respectively?

Solution: If the speed downstream is  a km/hr  and the speed upstream is  b km/hr , then

Speed in still water = (a + b)/2 km/h

Rate of stream = ½ (a − b) kmph

Let the Boat’s rate upstream be  x  kmph and that downstream be  y  kmph.

Then, distance covered upstream in 6 hrs 30 min = Distance covered downstream in 3 hrs.

⇒ x × 6.5 hrs = y × 3hrs

⇒ 13/2x = 3y

⇒ y = 13x/6

Frequently Asked Questions – FAQs

How to solve linear equation in two variables, how many solutions are there for linear equations in two variables, what is the two-variable equation, what are the coefficients of the equation 3x-6y = -13, what is the constant of the equation 3x-6y=-13.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Excellent service

excellent job

Helping the students well

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Systems of Linear Equations

Solve Systems of Linear Equations with Two Variables

Learning objectives.

By the end of this section, you will be able to:

• Determine whether an ordered pair is a solution of a system of equations
• Solve a system of linear equations by graphing
• Solve a system of equations by substitution
• Solve a system of equations by elimination
• Choose the most convenient method to solve a system of linear equations

Before you get started, take this readiness quiz.

Determine Whether an Ordered Pair is a Solution of a System of Equations

In Solving Linear Equations , we learned how to solve linear equations with one variable. Now we will work with two or more linear equations grouped together, which is known as a system of linear equations .

When two or more linear equations are grouped together, they form a system of linear equations .

In this section, we will focus our work on systems of two linear equations in two unknowns. We will solve larger systems of equations later in this chapter.

An example of a system of two linear equations is shown below. We use a brace to show the two equations are grouped together to form a system of equations.

To determine if an ordered pair is a solution to a system of two equations, we substitute the values of the variables into each equation. If the ordered pair makes both equations true, it is a solution to the system.

Solve a System of Linear Equations by Graphing

In this section, we will use three methods to solve a system of linear equations. The first method we’ll use is graphing.

The graph of a linear equation is a line. Each point on the line is a solution to the equation. For a system of two equations, we will graph two lines. Then we can see all the points that are solutions to each equation. And, by finding what the lines have in common, we’ll find the solution to the system.

Most linear equations in one variable have one solution, but we saw that some equations, called contradictions, have no solutions and for other equations, called identities, all numbers are solutions.

Similarly, when we solve a system of two linear equations represented by a graph of two lines in the same plane, there are three possible cases, as shown.

Each time we demonstrate a new method, we will use it on the same system of linear equations. At the end of the section you’ll decide which method was the most convenient way to solve this system.

The steps to use to solve a system of linear equations by graphing are shown here.

• Graph the first equation.
• Graph the second equation on the same rectangular coordinate system.
• Determine whether the lines intersect, are parallel, or are the same line.

If the lines intersect, identify the point of intersection. This is the solution to the system.

If the lines are parallel, the system has no solution.

• If the lines are the same, the system has an infinite number of solutions.
• Check the solution in both equations.

In the next example, we’ll first re-write the equations into slope–intercept form as this will make it easy for us to quickly graph the lines.

In all the systems of linear equations so far, the lines intersected and the solution was one point. In the next two examples, we’ll look at a system of equations that has no solution and at a system of equations that has an infinite number of solutions.

no solution

Sometimes the equations in a system represent the same line. Since every point on the line makes both equations true, there are infinitely many ordered pairs that make both equations true. There are infinitely many solutions to the system.

If you write the second equation in slope-intercept form, you may recognize that the equations have the same slope and same y -intercept.

infinitely many solutions

When we graphed the second line in the last example, we drew it right over the first line. We say the two lines are coincident . Coincident lines have the same slope and same y- intercept.

Coincident lines have the same slope and same y- intercept.

The systems of equations in (Figure) and (Figure) each had two intersecting lines. Each system had one solution.

In (Figure) , the equations gave coincident lines, and so the system had infinitely many solutions.

The systems in those three examples had at least one solution. A system of equations that has at least one solution is called a consistent system.

A system with parallel lines, like (Figure) , has no solution. We call a system of equations like this inconsistent. It has no solution.

A consistent system of equations is a system of equations with at least one solution.

An inconsistent system of equations is a system of equations with no solution.

We also categorize the equations in a system of equations by calling the equations independent or dependent . If two equations are independent, they each have their own set of solutions. Intersecting lines and parallel lines are independent.

If two equations are dependent, all the solutions of one equation are also solutions of the other equation. When we graph two dependent equations, we get coincident lines.

Let’s sum this up by looking at the graphs of the three types of systems. See below and (Figure) .

Without graphing, determine the number of solutions and then classify the system of equations.

ⓐ We will compare the slopes and intercepts of the two lines.

A system of equations whose graphs are parallel lines has no solution and is inconsistent and independent.

ⓑ We will compare the slope and intercepts of the two lines.

A system of equations whose graphs are intersect has 1 solution and is consistent and independent.

ⓐ no solution, inconsistent, independent ⓑ one solution, consistent, independent

Solve a System of Equations by Substitution

We will now solve systems of linear equations by the substitution method.

We will use the same system we used first for graphing.

We will first solve one of the equations for either x or y . We can choose either equation and solve for either variable—but we’ll try to make a choice that will keep the work easy.

Then we substitute that expression into the other equation. The result is an equation with just one variable—and we know how to solve those!

After we find the value of one variable, we will substitute that value into one of the original equations and solve for the other variable. Finally, we check our solution and make sure it makes both equations true.

• Solve one of the equations for either variable.
• Substitute the expression from Step 1 into the other equation.
• Solve the resulting equation.
• Substitute the solution in Step 3 into either of the original equations to find the other variable.
• Write the solution as an ordered pair.
• Check that the ordered pair is a solution to both original equations.

Be very careful with the signs in the next example.

We need to solve one equation for one variable. We will solve the first equation for y .

Solve a System of Equations by Elimination

We have solved systems of linear equations by graphing and by substitution. Graphing works well when the variable coefficients are small and the solution has integer values. Substitution works well when we can easily solve one equation for one of the variables and not have too many fractions in the resulting expression.

The third method of solving systems of linear equations is called the Elimination Method. When we solved a system by substitution, we started with two equations and two variables and reduced it to one equation with one variable. This is what we’ll do with the elimination method, too, but we’ll have a different way to get there.

The Elimination Method is based on the Addition Property of Equality. The Addition Property of Equality says that when you add the same quantity to both sides of an equation, you still have equality. We will extend the Addition Property of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For any expressions a, b, c, and d .

To solve a system of equations by elimination, we start with both equations in standard form. Then we decide which variable will be easiest to eliminate. How do we decide? We want to have the coefficients of one variable be opposites, so that we can add the equations together and eliminate that variable.

Notice how that works when we add these two equations together:

The y ’s add to zero and we have one equation with one variable.

Let’s try another one:

This time we don’t see a variable that can be immediately eliminated if we add the equations.

Then rewrite the system of equations.

Now we see that the coefficients of the x terms are opposites, so x will be eliminated when we add these two equations.

Once we get an equation with just one variable, we solve it. Then we substitute that value into one of the original equations to solve for the remaining variable. And, as always, we check our answer to make sure it is a solution to both of the original equations.

Now we’ll see how to use elimination to solve the same system of equations we solved by graphing and by substitution.

The steps are listed here for easy reference.

• Write both equations in standard form. If any coefficients are fractions, clear them.

Decide which variable you will eliminate.

• Multiply one or both equations so that the coefficients of that variable are opposites.
• Add the equations resulting from Step 2 to eliminate one variable.
• Solve for the remaining variable.
• Substitute the solution from Step 4 into one of the original equations. Then solve for the other variable.

Now we’ll do an example where we need to multiply both equations by constants in order to make the coefficients of one variable opposites.

In this example, we cannot multiply just one equation by any constant to get opposite coefficients. So we will strategically multiply both equations by different constants to get the opposites.

When the system of equations contains fractions, we will first clear the fractions by multiplying each equation by the LCD of all the fractions in the equation.

In this example, both equations have fractions. Our first step will be to multiply each equation by the LCD of all the fractions in the equation to clear the fractions.

When we solved the system by graphing, we saw that not all systems of linear equations have a single ordered pair as a solution. When the two equations were really the same line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent system.

The same is true using substitution or elimination. If the equation at the end of substitution or elimination is a true statement, we have a consistent but dependent system and the system of equations has infinitely many solutions. If the equation at the end of substitution or elimination is a false statement, we have an inconsistent system and the system of equations has no solution.

This is a true statement. The equations are consistent but dependent. Their graphs would be the same line. The system has infinitely many solutions.

After we cleared the fractions in the second equation, did you notice that the two equations were the same? That means we have coincident lines.

Choose the Most Convenient Method to Solve a System of Linear Equations

When you solve a system of linear equations in in an application, you will not be told which method to use. You will need to make that decision yourself. So you’ll want to choose the method that is easiest to do and minimizes your chance of making mistakes.

For each system of linear equations, decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

Since both equations are in standard form, using elimination will be most convenient.

Since one equation is already solved for y , using substitution will be most convenient.

For each system of linear equations decide whether it would be more convenient to solve it by substitution or elimination. Explain your answer.

ⓐ Since both equations are in standard form, using elimination will be most convenient. ⓑ Since one equation is already solved for x , using substitution will be most convenient.

ⓐ Since one equation is already solved for y , using substitution will be most convenient. ⓑ Since both equations are in standard form, using elimination will be most convenient.

Key Concepts

Practice Makes Perfect

In the following exercises, determine if the following points are solutions to the given system of equations.

In the following exercises, solve the following systems of equations by graphing.

infinite solutions

1 point, consistent and independent

infinite solutions, consistent, dependent

In the following exercises, solve the systems of equations by substitution.

In the following exercises, solve the systems of equations by elimination.

infinitely many

In the following exercises, decide whether it would be more convenient to solve the system of equations by substitution or elimination.

ⓐ substitution ⓑ elimination

ⓐ elimination ⓑ substituion

Writing Exercises

In a system of linear equations, the two equations have the same intercepts. Describe the possible solutions to the system.

Answers will vary.

ⓐ by graphing ⓑ by substitution

After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

If most of your checks were:

…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.

…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?

…no – I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Intermediate Algebra Copyright © 2017 by OSCRiceUniversity is licensed under a Creative Commons Attribution 4.0 International License , except where otherwise noted.

Share This Book